🧪 pytest-bootstrap¶

Scientific software development often relies on stochasticity, e.g. for Monte Carlo integration or simulating the Ising model. Testing non-deterministic code is difficult. This package offers a bootstrap test to validate stochastic algorithms, including multiple hypothesis correction for vector statistics. It can be installed by running pip install pytest-bootstrap.
Example¶
Suppose we want to implement the expected value of log-normal distribution with location parameter \(\mu\) and scale parameter \(\sigma\).
>>> import numpy as np
>>>
>>> def lognormal_expectation(mu, sigma):
... return np.exp(mu + sigma ** 2 / 2)
>>>
>>> def lognormal_expectation_wrong(mu, sigma):
... return np.exp(mu + sigma ** 2)
We can validate our implementation by simulating from a lognormal distribution and comparing with the bootstrapped mean.
>>> from pytest_bootstrap import bootstrap_test
>>>
>>> mu = -1
>>> sigma = 1
>>> reference = lognormal_expectation(mu, sigma)
>>> x = np.exp(np.random.normal(mu, sigma, 1000))
>>> result = bootstrap_test(x, np.mean, reference)
This returns a summary of the test, such as the bootstrapped statistics.
>>> result.keys()
dict_keys(['alpha', 'alpha_corrected', 'reference', 'lower', 'upper',
'z_score', 'median', 'iqr', 'tol', 'statistics'])
Comparing with our incorrect implementation reveals the bug.
>>> reference_wrong = lognormal_expectation_wrong(mu, sigma)
>>> result = bootstrap_test(x, np.mean, reference_wrong)
Traceback (most recent call last):
...
pytest_bootstrap.BootstrapTestError: the reference value 1.0 lies outside
the 1 - (alpha = 0.01) interval ...
Visualising the bootstrapped distribution using pytest_bootstrap.result_hist() can help identify discrepancies between the bootstrapped statistics and the theoretical reference value. Note that you need to install matplotlib separately or install pytest-bootstrap using pip install pytest-bootstrap[plot].
(Source code, png)
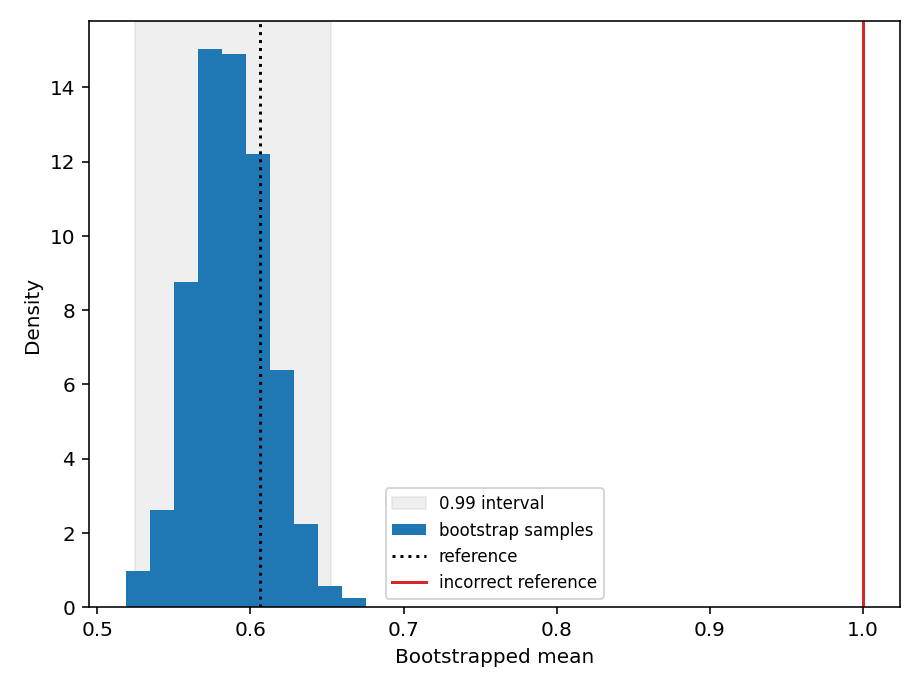
Histogram of bootstrapped means reveals the erroneous implementation of the log-normal mean.¶
A comprehensive set of examples can be found in the tests.
Interface¶
- exception pytest_bootstrap.BootstrapTestError(result: dict)¶
Reference value falls outside bootstrapped confidence interval.
- pytest_bootstrap.bootstrap_test(samples: numpy.ndarray, statistic: Callable, reference: float, statistic_args: Optional[Iterable] = None, statistic_kwargs: Optional[Mapping] = None, num_bootstrap_samples: int = 1000, alpha: float = 0.01, multiple_hypothesis_correction: str = 'bonferroni', rtol: float = 1e-07, atol: float = 0, on_fail: str = 'raise') dict¶
Compare a bootstrap sample of a
statisticevaluated on i.i.dsamplesfrom a stochastic process with areferencevalue.The test will fail if the
referencelies outside the1 - alphaposterior interval, i.e. is smaller than the empiricalalpha / 2quantile or larger than the1 - alpha / 2quantile. The relativertoland absolute toleranceatolare added together to obtain an overall toleranceatol + rtol * abs(reference)for the interval test (seenumpy.isclose()for further details).- Parameters
samples – I.i.d. samples from a stochastic process on which to evaluate the
statistic.statistic – Function to evaluate a statistic on a bootstrapped sample.
reference – Reference value to compare with the bootstrap sample of the
statistic.statistic_args – Positional arguments forwarded to the
statistic.statistic_kwargs – Keyword arguments forwarded to the
statistic.num_bootstrap_samples – Number of bootstrap samples.
alpha – Significance level to use for testing agreement between the bootstrapped distribution of the
statisticand thereferencevalue.alpharoughly corresponds to the probability that the test will fail even if thereferencevalue is correct. This value should be small for the test to pass with high probability.multiple_hypothesis_correction – Method used to correct for multiple hypotheses being tested if the statistic is vector-valued.
Falsedisables multiple hypothesis correction.rtol – Relative tolerance.
atol – Absolute tolerance.
on_fail – Raise a
BootstrapTestErrorifraiseor warn ifwarn.
- Returns
result – Dictionary of test information, comprising
alpha_corrected– Significance level after multiple hypothesis correction. Equal toalphaif the statistic is a scalar or no multiple hypothesis correction is applied.lower– Lower limit of the1 - alphabootstrapped interval, i.e. thealpha / 2quantile.upper– Upper limit of the1 - alphabootstrapped interval, i.e. the1 - alpha / 2quantile.iqr– Interquartile range of the bootstrappedstatistic.median– Median of the bootstrappedstatistic.z_score– Z-score of thereferencevalue under the bootstrapped distribution, i.e.(reference - mean(s)) / std(s), wheresis the vector of bootstrappedstatistic.
- pytest_bootstrap.result_hist(result: dict, show_interval: bool = True, ax=None, **kwargs) None¶
Plot a histogram of bootstrapped statistics together with the reference value and \(1 - \alpha\) interval.
Note
Use
on_fail = 'warn'as an argument tobootstrap_test()to obtain test results for a failing test.- Parameters
result – Bootstrap test result generated by
bootstrap_test().show_interval – Whether to show the \(1 - \alpha\) interval.
ax – Axes to use for plotting